Ce este o bisectoare?
Bisectoarea unui unghi al unui triunghi este semidreapta care împarte unghiul respectiv în două unghiuri congruente. Aceasta pornește din vârful unghiului și intersectează latura opusă.
Enunțul Teoremei Bisectoarei
Într-un triunghi, bisectoarea unui unghi împarte latura opusă în segmente proporționale cu lungimile laturilor care formează unghiul respectiv.
Matematic, pentru un triunghi \( \triangle ABC \) cu bisectoarea \( AD \), unde \( D \) este punctul de pe latura \( BC \), avem relația:
\[ \frac{BD}{DC} = \frac{AB}{AC} \]
Demonstratie
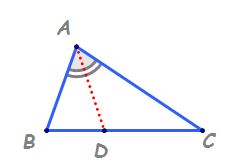
- Se consideră \( \triangle ABC \) cu bisectoarea \( AD \).
- Prin construcție, \( \angle BAD = \angle CAD \).
- Se construiește o paralelă la \( BC \), care trece prin punctul \( A \).
- Se aplică teorema asemănării triunghiurilor, de unde rezultă raportul proporțional.
Consecințe ale Teoremei Bisectoarei
- Bisectoarea împarte triunghiul în două triunghiuri mai mici, asemănătoare cu triunghiul original.
- Relația dintre segmentele create de bisectoare și laturile triunghiului oferă o metodă de calcul pentru segmentele necunoscute.
Exemplu de aplicare
În \( \triangle ABC \), se cunoaște că \( AB = 8 \, \text{cm} \), \( AC = 6 \, \text{cm} \), iar bisectoarea \( AD \) intersectează latura \( BC \) în \( D \), astfel încât \( BD = 4 \, \text{cm} \). Calculați lungimea \( DC \).
Răspuns:
Conform teoremei bisectoarei: \[ \frac{BD}{DC} = \frac{AB}{AC} \] \[ \frac{4}{DC} = \frac{8}{6} \] Rezolvând: \[ DC = 3 \, \text{cm} \]
Exerciții
1
Într-un triunghi \( \triangle ABC \), se cunoaște că \( AB = 10 \, \text{cm} \), \( AC = 15 \, \text{cm} \), iar bisectoarea \( AD \) împarte \( BC \) în \( BD = 6 \, \text{cm} \). Determinați lungimea segmentului \( DC \).
2
Într-un triunghi \( \triangle XYZ \), bisectoarea \( XM \) intersectează latura \( YZ \) în \( M \). Se știe că \( XY = 9 \, \text{cm} \), \( XZ = 12 \, \text{cm} \) și \( YZ = 10 \, \text{cm} \). Calculați segmentele \( YM \) și \( MZ \).
3
Într-un triunghi dreptunghic \( \triangle ABC \), unghiul \( \angle B = 90^\circ \). Bisectoarea \( BD \) împarte latura \( AC \) în \( AD = 5 \, \text{cm} \) și \( DC = 4 \, \text{cm} \). Determinați lungimile \( AB \) și \( BC \).
4
În \( \triangle DEF \), bisectoarea \( DM \) împarte \( EF \) în segmente proporționale. Se știe că \( EF = 14 \, \text{cm} \), \( DE = 8 \, \text{cm} \), și \( DF = 10 \, \text{cm} \). Determinați lungimile \( EM \) și \( MF \).
5
Într-un triunghi isoscel \( \triangle ABC \), unde \( AB = AC = 12 \, \text{cm} \), iar baza \( BC = 10 \, \text{cm} \). Bisectoarea \( AD \) împarte \( BC \) în două segmente. Determinați lungimile segmentelor \( BD \) și \( DC \).
6
În \( \triangle GHI \), se știe că \( GH = 7 \, \text{cm} \), \( GI = 5 \, \text{cm} \), iar bisectoarea \( GM \) intersectează latura \( HI \). Lungimea segmentului \( HI \) este \( 9 \, \text{cm} \). Determinați lungimile \( HM \) și \( MI \).
7
În \( \triangle PQR \), bisectoarea \( PS \) împarte latura \( QR \) în două segmente, astfel încât \( QS = 3x \) și \( SR = 2x \). Dacă \( PQ = 9 \, \text{cm} \) și \( PR = 6 \, \text{cm} \), determinați lungimile segmentelor \( QS \) și \( SR \).
8
Într-un triunghi dreptunghic \( \triangle ABC \), unghiul \( \angle B = 90^\circ \). Bisectoarea \( BD \) împarte latura \( AC \) în segmente egale. Se știe că \( AB = 8 \, \text{cm} \) și \( BC = 6 \, \text{cm} \). Calculați lungimea \( AC \).
9
Într-un triunghi \( \triangle XYZ \), bisectoarea \( XM \) împarte latura \( YZ \) în \( YM = 6 \, \text{cm} \) și \( MZ = 9 \, \text{cm} \). Dacă \( XY = 8 \, \text{cm} \), calculați lungimea \( XZ \).
10
În \( \triangle ABC \), bisectoarea \( AD \) împarte \( BC \) în două segmente proporționale cu laturile \( AB \) și \( AC \). Se știe că \( AB = 11 \, \text{cm} \), \( AC = 9 \, \text{cm} \), și \( BC = 10 \, \text{cm} \). Calculați lungimile \( BD \) și \( DC \).
