Triunghi dreptunghic
1. Noțiuni de bază
Un triunghi dreptunghic este un triunghi care are un unghi drept, adică un unghi de \( 90^\circ \).
Elementele triunghiului dreptunghic:
- Catetele: laturile care formează unghiul drept.
- Ipotenuza: latura opusă unghiului drept și cea mai lungă latură a triunghiului.
2. Teorema lui Pitagora
Într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor catetelor:
\( a^2 + b^2 = c^2 \)
Unde:
- \( a, b \): catetele triunghiului;
- \( c \): ipotenuza.
Exemplu: Dacă \( a = 3 \) și \( b = 4 \), atunci ipotenuza \( c \) este:
\( c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \).
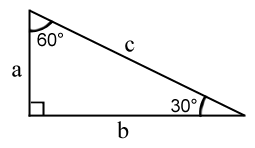
3. Proprietatea triunghiului cu un unghi de \( 30^\circ \)
Într-un triunghi dreptunghic care are un unghi de \( 30^\circ \), cateta opusă unghiului de \( 30^\circ \) este jumătate din ipotenuză:
\(\displaystyle a = \frac{c}{2} \)
\(\displaystyle c = 2 \cdot a \).
4. Proprietatea triunghiului cu un unghi de \( 45^\circ \)
Într-un triunghi dreptunghic cu un unghi de \( 45^\circ \), catetele sunt egale:
\( a = b \).
5. Mediana dusă pe ipotenuză
Într-un triunghi dreptunghic, mediana dusă pe ipotenuză este jumătate din lungimea ipotenuzei:
\( m = \frac{i}{2} \).
Exemplu: Dacă ipotenuza are lungimea \( 10 \), atunci mediana dusă pe ipotenuză este:
\( m = \frac{10}{2} = 5 \).
Rezumat
- Triunghiul dreptunghic are un unghi drept (\( 90^\circ \));
- Teorema lui Pitagora: \( c_1^2 + c_2^2 = i^2 \);
- Unghi de \( 30^\circ \): \( C_{30^\circ} = \frac{i}{2} \), \( L = 2 \cdot C_{30^\circ} \);
- Unghi de \( 45^\circ \): \( c_1 = c_2 \), \( i = c_1\sqrt{2} \);
- Mediana dusă pe ipotenuză: \( m = \frac{i}{2} \).