Linii importante in triunghi

Triunghiul are mai multe linii importante, fiecare având proprietăți și roluri specifice. Acestea sunt:

1. Înălțimea

Înălțimea unui triunghi este segmentul perpendicular dus dintr-un vârf al triunghiului pe latura opusă sau pe prelungirea acesteia.

  • Triunghiul are trei înălțimi, câte una corespunzătoare fiecărei laturi.
  • Punctul de intersecție al înălțimilor se numește ortocentru.
Înălțimea unui triunghi

2. Mediana

Mediana este segmentul de dreaptă care unește un vârf al triunghiului cu mijlocul laturii opuse.

  • Triunghiul are trei mediane.
  • Punctul de intersecție al medianelor se numește centroid, care împarte fiecare mediană în raportul 2:1.
Mediana unui triunghi

3. Bisectoarea

Bisectoarea este segmentul de dreaptă care împarte un unghi al triunghiului în două părți egale.

  • Triunghiul are trei bisectoare, câte una pentru fiecare unghi.
  • Punctul de intersecție al bisectoarelor se numește centrul cercului înscris.
Bisectoarea unui triunghi

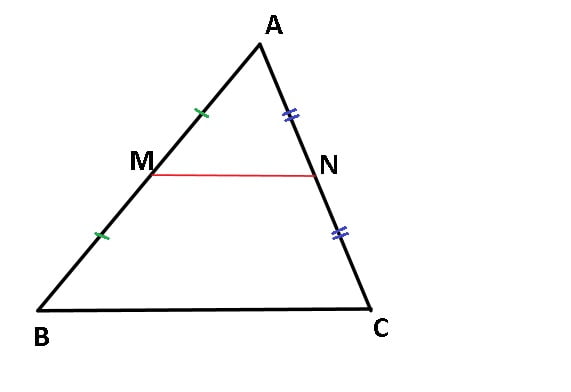
4. Linia mijlocie

Linia mijlocie este segmentul care unește mijloacele a două laturi ale triunghiului.

  • Triunghiul are trei linii mijlocii.
  • Linia mijlocie este paralelă cu a treia latură și are jumătate din lungimea acesteia.
Linia mijlocie a unui triunghi

Concluzie

Liniile importante ale triunghiului sunt esențiale în studiul geometriei și au aplicații în diverse probleme practice și teoretice.

Exerciții

1
Într-un triunghi \(ABC\), înălțimea din vârful \(A\) pe baza \(BC\) are lungimea de \(8 \, \text{cm}\). Dacă \(BC = 12 \, \text{cm}\), calculați aria triunghiului.
2
Fie triunghiul \(ABC\), cu baza \(BC = 10 \, \text{cm}\). Mediana dusă din \(A\) către mijlocul laturii \(BC\) are lungimea de \(7 \, \text{cm}\). Determinați lungimea medianei dusă din \(B\) pe \(AC\), dacă triunghiul este isoscel cu \(AB = AC\).
3
Într-un triunghi \(ABC\), bisectoarea unghiului \(A\) intersectează latura \(BC\) în punctul \(D\). Dacă \(AB = 9 \, \text{cm}\), \(AC = 12 \, \text{cm}\) și \(BC = 15 \, \text{cm}\), determinați lungimea segmentului \(BD\).
4
Linia mijlocie trasată între mijloacele laturilor \(AB\) și \(AC\) ale unui triunghi \(ABC\) are lungimea de \(6 \, \text{cm}\). Determinați lungimea bazei \(BC\).
5
Într-un triunghi dreptunghic \(ABC\) cu unghiul drept în \(B\), ipotenuza \(AC = 13 \, \text{cm}\). Înălțimea trasată din \(B\) pe \(AC\) împarte ipotenuza în segmente de lungimi \(5 \, \text{cm}\) și \(8 \, \text{cm}\). Verificați corectitudinea datelor folosind teorema lui Pitagora.
6
Fie triunghiul \(ABC\) cu laturile \(AB = 7 \, \text{cm}\), \(AC = 9 \, \text{cm}\), \(BC = 12 \, \text{cm}\). Determinați coordonatele centrului cercului înscris dacă triunghiul este într-un sistem cartezian cu \(A(0, 0)\), \(B(7, 0)\), \(C(x, y)\).
7
Într-un triunghi echilateral, fiecare mediana are lungimea \(10 \, \text{cm}\). Calculați lungimea unei laturi a triunghiului.
8
Într-un triunghi \(ABC\), mediana trasată din \(A\) către \(BC\) și bisectoarea unghiului \(A\) coincid. Dacă \(AB = AC\), demonstrați că triunghiul este isoscel.
9
Linia mijlocie trasată între mijloacele laturilor \(AB\) și \(BC\) ale unui triunghi \(ABC\) este paralelă cu latura \(AC\) și are lungimea de \(4 \, \text{cm}\). Calculați lungimea lui \(AC\).
10
Într-un triunghi \(ABC\), înălțimile se intersectează într-un punct numit ortocentru. Demonstrați că înălțimile unui triunghi dreptunghic se intersectează chiar pe ipotenuză.
Înapoi Următor