Triunghi dreptunghic
1. Noțiuni de bază
Un triunghi dreptunghic este un triunghi care are un unghi drept, adică un unghi de \( 90^\circ \).
Elementele triunghiului dreptunghic:
- Catetele: laturile care formează unghiul drept.
- Ipotenuza: latura opusă unghiului drept și cea mai lungă latură a triunghiului.
2. Teorema lui Pitagora
Într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor catetelor:
\( a^2 + b^2 = c^2 \)
Unde:
- \( a, b \): catetele triunghiului;
- \( c \): ipotenuza.
Exemplu: Dacă \( a = 3 \) și \( b = 4 \), atunci ipotenuza \( c \) este:
\( c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \).
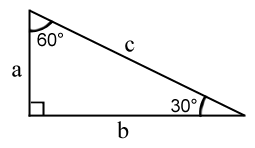
3. Proprietatea triunghiului cu un unghi de \( 30^\circ \)
Într-un triunghi dreptunghic care are un unghi de \( 30^\circ \), cateta opusă unghiului de \( 30^\circ \) este jumătate din ipotenuză:
\(\displaystyle a = \frac{c}{2} \)
\(\displaystyle c = 2 \cdot a \).
4. Proprietatea triunghiului cu un unghi de \( 45^\circ \)
Într-un triunghi dreptunghic cu un unghi de \( 45^\circ \), catetele sunt egale:
\( a = b \)
5. Mediana dusă pe ipotenuză
Într-un triunghi dreptunghic, mediana dusă pe ipotenuză este jumătate din lungimea ipotenuzei:
\(\displaystyle m = \frac{c}{2} \)
Exemplu: Dacă ipotenuza are lungimea \( 10 \), atunci mediana dusă pe ipotenuză este:
\( m = \frac{10}{2} = 5 \).
6. Aria triunghiului dreptunghic
unde a, b - sunt catetele triunghiului
7. Alte teoreme
Teorema Înălțimii
\( AD^2 = BD \cdot DC \)
Unde:
- \( AD \): înălțimea dusă pe ipotenuză;
- \( BD, DC \): proiecțiile catetelor pe ipotenuză.
Teorema Catetei
\( AB^2 = BC \cdot BD \)
Unde:
- \( AB \): cateta;
- \( BC \): ipotenuza;
- \( BD \): proiecția catetei \( a \) pe ipotenuză.
Problema rezolvata
Fie triunghiul dreptunghic \( \triangle ABC \), în care \( m(\angle C) = 90^\circ \), iar \( AC = 6 \, \text{cm} \). Determinați aria triunghiului \( \triangle ABC \), dacă se cunoaște că perimetrul său este egal cu \( 24 \, \text{cm} \).
Perimetrul triunghiului este: \[ P_{\triangle ABC} = AB + BC + AC = 24 \implies AB + BC + 6 = 24 \implies AB + BC = 18 \]
Folosim formula ariei triunghiului dreptunghic:
\[ A_{\triangle ABC} = \frac{AC \cdot BC}{2} \]Aplicăm teorema lui Pitagora în \( \triangle ABC \):
\[ AB^2 = AC^2 + BC^2 \implies (18 - BC)^2 = 36 + BC^2 \]Rezolvând ecuația:
\[ 324 - 36 \cdot BC + BC^2 = 36 + BC^2 \implies 324 - 36 \cdot BC - 36 = 0 \] \[ -36 \cdot BC + 288 = 0 \implies BC = \frac{288}{36} = 8 \, \text{cm} \]Calculăm aria triunghiului:
\[ A_{\triangle ABC} = \frac{6 \cdot 8}{2} = 24 \, \text{cm}^2 \]